Quartiles, Quartile Deviation and Quartile co-efficient

The Quartile Deviation is a simple way to estimate the spread of a distribution about a measure of its central tendency (usually the mean). So, it gives you an idea about the range within which the central 50% of your sample data lies. Consequently, based on the quartile deviation, the Coefficient of Quartile Deviation can be defined, which makes it easy to compare the spread of two or more different distributions. Since both of these topics are based on the concept of quartiles, we’ll first understand how to calculate the quartiles of a dataset before working with the direct formulae.

Quartiles

A median divides a given dataset (which is already sorted) into two equal halves similarly, the quartiles are used to divide a given dataset into four equal halves. Therefore, logically there should be three quartiles for a given distribution, but if you think about it, the second quartile is equal to the median itself! We’ll deal with the other two quartiles in this section.

• The first quartileor the lower quartile or the 25th percentile, also denoted by Q₁, corresponds to the value that lies halfway between the median and the lowest value in the distribution (when it is already sorted in the ascending order). Hence, it marks the region which encloses 25% of the initial data.
• Similarly, the third quartileor the upper quartile or 75th percentile, also denoted by Q3, corresponds to the value that lies halfway between the median and the highest value in the distribution (when it is already sorted in the ascending order). It, therefore, marks the region which encloses the 75% of the initial data or 25% of the end data.

For a better understanding, look at the representation below for a Gaussian Distribution:

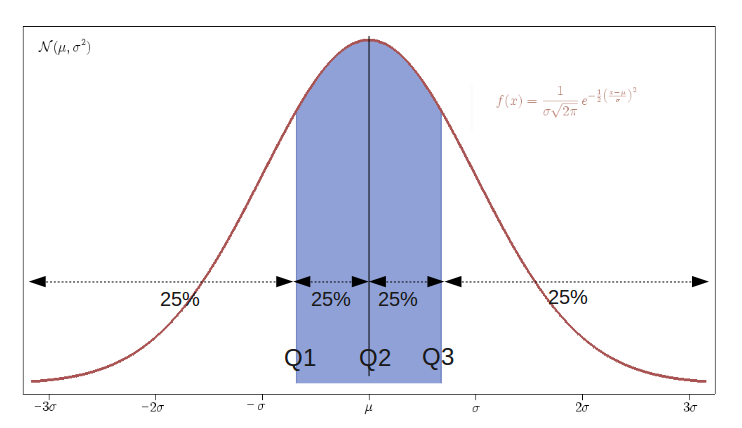
The Quartile Deviation

Formally, the Quartile Deviation is equal to the half of the Inter-Quartile Range and thus we can write it as:

Qd=(Q3–Q1)/2

Therefore, we also call it the Semi Inter-Quartile Range.

• The Quartile Deviation doesn’t take into account the extreme points of the distribution. Thus, the dispersion or the spread of only the central 50% data is considered.
• If the scale of the data is changed, the Qd also changes in the same ratio.
• It is the best measure of dispersion for open-ended systems (which have open-ended extreme ranges).
• Also, it is less affected by sampling fluctuations in the dataset as compared to the range (another measure of dispersion).
• Since it is solely dependent on the central values in the distribution, if in any experiment, these values are abnormal or inaccurate, the result would be affected drastically.

The Coefficient of Quartile Deviation

Based on the quartiles, a relative measure of dispersion, known as the Coefficient of Quartile Deviation, can be defined for any distribution. It is formally defined as:

Coefficient of Quartile Deviation = {(Q3–Q1)/(Q3+Q1)}×100

Since it involves a ratio of two quantities of the same dimensions, it is unit-less. Thus, it can act as a suitable parameter for comparing two or more different datasets which may or may not involve quantities with the same dimensions.

So, now let’s go through the solved examples below to get a better idea of how to apply these concepts to various distributions.