Tag: Inferential Statistics

Management Notes

Calculation of EMI

indiafreenotesby indiafreenotes0

Equated Monthly Installment (EMI) is the fixed payment amount borrowers make to lenders each month to repay a loan. EMIs consist of both the principal and the interest, and the amount remains constant throughout the loan tenure. The formula for calculating EMI is:

where:

  • P = Principal amount (loan amount),
  • r = Monthly interest rate (annual interest rate divided by 12 and expressed as a decimal),
  • n = Number of monthly installments (loan tenure in months).

Components of EMI Calculation:

  • Principal (P):

This is the amount initially borrowed from the lender. It’s the base amount on which interest is calculated. Higher principal amounts lead to higher EMIs, as the overall amount owed is greater.

  • Interest Rate (r):

The rate of interest applied to the principal impacts the EMI significantly. Interest rate is typically given annually but needs to be converted into a monthly rate for EMI calculations. For instance, a 12% annual rate would be converted to a 1% monthly rate (12% ÷ 12).

  • Loan Tenure (n):

The number of months over which the loan is repaid. A longer tenure reduces the monthly EMI amount because the total loan repayment is spread over a greater number of installments, though this may lead to higher total interest paid.

Types of EMI Calculation Methods:

  • Flat Rate EMI:

Here, interest is calculated on the original principal amount throughout the tenure. The formula differs from the reducing balance method and generally results in higher EMIs.

  • Reducing Balance EMI:

This is the most common method for EMI calculations, where interest is calculated on the outstanding balance. As the principal reduces over time, interest payments decrease, leading to an overall lower cost compared to the flat rate.

Importance of EMI Calculation:

  • Assess Affordability:

Borrowers can determine if the EMI amount fits within their monthly budget, ensuring they can make payments consistently.

  • Plan Finances:

Knowing the EMI in advance helps in planning for other financial obligations and expenses.

  • Compare Loan Options:

Borrowers can evaluate different loan offers by comparing EMIs for similar loan amounts and tenures but with varying interest rates.

Management Notes

Sinking Fund, Purpose, Structure, Benefits, Applications

indiafreenotesby indiafreenotes0

Sinking Fund is a financial mechanism used to set aside money over time for the purpose of repaying debt or replacing a significant asset. It acts as a savings plan that allows an organization or individual to accumulate funds for a specific future obligation, ensuring that they have enough resources to meet that obligation without straining their financial situation.

Purpose of a Sinking Fund:

The primary purpose of a sinking fund is to manage debt repayment or asset replacement efficiently.

  • Reduce Default Risk:

By setting aside funds regularly, borrowers can reduce the risk of default on their obligations. This practice assures lenders that the borrower is financially responsible and prepared to meet repayment terms.

  • Facilitate Large Purchases:

For organizations, sinking funds can help manage significant future expenditures, such as replacing machinery, vehicles, or technology. This ensures that funds are available when needed, mitigating the impact on cash flow.

  • Enhance Financial Planning:

Establishing a sinking fund encourages better financial planning and discipline. Organizations can forecast their future cash requirements, making it easier to allocate resources appropriately.

Structure of a Sinking Fund:

  • Regular Contributions:

The entity responsible for the sinking fund makes regular contributions, typically monthly or annually. The amount of these contributions can be fixed or variable based on a predetermined plan.

  • Interest Earnings:

The contributions are usually invested in low-risk securities or interest-bearing accounts. This investment allows the sinking fund to grow over time through interest earnings, ultimately increasing the amount available for future obligations.

  • Target Amount:

The sinking fund is established with a specific target amount that reflects the total debt or asset replacement cost. The time frame for reaching this target is also defined, ensuring that contributions align with the due date for the obligation.

Benefits of a Sinking Fund:

  • Financial Stability:

By accumulating funds over time, sinking funds contribute to financial stability, reducing the pressure to secure large amounts of money at once.

  • Improved Creditworthiness:

A well-managed sinking fund can enhance an organization’s credit rating. Lenders view sinking funds as a positive indicator of an entity’s ability to manage its debts responsibly.

  • Cost Management:

Sinking funds help manage the cost of large purchases or debt repayments by spreading the financial burden over time, reducing the impact on cash flow.

  • Flexibility:

The structure of a sinking fund can be adjusted based on changing financial circumstances. Contributions can be increased or decreased as needed, providing flexibility in financial planning.

  • Risk Mitigation:

By setting aside funds in advance, entities can mitigate the risks associated with sudden financial obligations, ensuring they are prepared for unexpected expenses or economic downturns.

Practical Applications of Sinking Funds:

  • Corporate Bonds:

Many corporations issue bonds that require a sinking fund to be established. The company sets aside money regularly to repay bondholders at maturity or periodically throughout the life of the bond.

  • Municipal Bonds:

Local governments often use sinking funds to repay municipal bonds. This practice ensures that they can meet their obligations without significantly impacting their budgets.

  • Asset Replacement:

Businesses may establish sinking funds for replacing equipment or vehicles. By planning ahead, they can avoid large capital outlays and maintain operations without disruption.

  • Real Estate:

Property management companies may set up sinking funds for the maintenance and eventual replacement of common areas or amenities within residential complexes.

  • Educational Institutions:

Schools and universities may use sinking funds to save for future building projects or major renovations, ensuring they can finance these endeavors without resorting to debt.

Management Notes

Perpetuity, Function

indiafreenotesby indiafreenotes0

Perpetuity refers to a financial instrument or cash flow that continues indefinitely without an end. In simpler terms, it is a stream of cash flows that occurs at regular intervals for an infinite duration. The present value of a perpetuity can be calculated using the formula:

PV = C/ r

Where,

C is the cash flow per period

r is the discount rate.

The concept of perpetuity has several important functions in finance and investment analysis. Here are eight key functions of perpetuity:

  • Valuation of Investments:

Perpetuity provides a method for valuing investments that generate constant cash flows over an indefinite period. This is particularly useful in valuing companies, real estate, and other assets that are expected to generate steady income streams indefinitely. By calculating the present value of these cash flows, investors can determine the fair value of such assets.

  • Determining Fixed Income Securities:

Perpetuities are often used in valuing fixed income securities like preferred stocks and bonds that pay a constant dividend or interest indefinitely. Investors can assess the attractiveness of these securities by comparing their present value to the market price, thus aiding investment decisions.

  • Simplifying Financial Analysis:

The concept of perpetuity simplifies complex financial models by allowing analysts to consider cash flows that extend indefinitely. This simplification is particularly valuable in scenarios where cash flows are expected to remain constant over a long period, providing a clearer picture of an investment’s worth.

  • Corporate Valuation:

In corporate finance, perpetuity is a critical component of valuation models, such as the Gordon Growth Model, which estimates the value of a company based on its expected future dividends. By considering dividends as a perpetuity, analysts can derive a more accurate valuation for firms with stable dividend policies.

  • Real Estate Investment:

In real estate, perpetuity helps in evaluating properties that generate consistent rental income. Investors can use the perpetuity formula to estimate the present value of future rental cash flows, facilitating better decision-making regarding property purchases or investments.

  • Retirement Planning:

Perpetuity can assist individuals in planning for retirement. By understanding how much they can withdraw from their retirement savings while maintaining a sustainable income level indefinitely, retirees can ensure financial security throughout their retirement years.

  • Life Insurance Valuation:

Perpetuities play a role in life insurance products that provide lifelong benefits. The present value of future benefits can be calculated using the perpetuity concept, aiding insurers in pricing their products and ensuring they can meet future obligations.

  • Evaluating Charitable Donations:

Nonprofit organizations can benefit from the concept of perpetuity when structuring endowments or perpetual funds. These funds are designed to provide a steady stream of income for ongoing operations, scholarships, or charitable initiatives. By understanding the present value of these perpetual cash flows, organizations can make informed decisions about resource allocation and fund management.

Bangalore University B.com Notes

Business Quantitative Analysis 1st Semester BU B.Com SEP Notes

indiafreenotesby indiafreenotes1
Unit 1,2,3,4 Pl. Refer Books Book

 

Unit 5 [Book]
Definition of Interest and Other Terms: Simple Interest and Compound Interest VIEW
Effective rate of Interest:
Present Value VIEW
Future Value VIEW
Perpetuity VIEW
Annuity VIEW
Sinking Fund VIEW
Valuation of Bonds VIEW
Calculating of EMI VIEW

 

Bangalore University B.com Notes

Business Mathematics & Statistics Bangalore University B.com 3rd Semester NEP Notes

indiafreenotesby indiafreenotes1
Unit 1 Commercial Arithmetic [Book]
Percentage VIEW
Cost, Profit and Selling price VIEW
Ratio Proportion VIEW
Problems on Speed and Time VIEW
Interest-Simple interest and Compound interest VIEW
Annuity VIEW

 

Unit 2 Theory of Equations [Book] No Update

 

Unit 3 Matrices and Determinants [Book] No Update

 

Unit 4 Measures of Central Tendency and Dispersion [Book]
Introduction Meaning and Definition, Objectives of measures of Central tendency VIEW
Types of averages: Arithmetic mean (Simple average only) VIEW
Median VIEW
Mode VIEW
Meaning and Objectives of measures of Dispersion VIEW
VIEW VIEW
Standard deviation and coefficient of Variation VIEW
Skewness VIEW VIEW
Problems on Direct method only VIEW

 

Unit 5 Correlation and Regression [Book]
Correlation: Meaning and definition-uses VIEW VIEW
VIEW
Karl Pearson’s coefficient of correlation (deviation from actual mean only) VIEW
Spearman’s Rank Correlation Coefficient VIEW
Regression Meaning VIEW
Regression Equations, Estimating x and y values VIEW
Finding correlation coefficient with Regression coefficient VIEW VIEW
Management Notes

Normal Distribution: Importance, Central Limit Theorem

indiafreenotesby indiafreenotes2

Normal distribution, or the Gaussian distribution, is a fundamental probability distribution that describes how data values are distributed symmetrically around a mean. Its graph forms a bell-shaped curve, with most data points clustering near the mean and fewer occurring as they deviate further. The curve is defined by two parameters: the mean (μ) and the standard deviation (σ), which determine its center and spread. Normal distribution is widely used in statistics, natural sciences, and social sciences for analysis and inference.

The general form of its probability density function is:

The parameter μ is the mean or expectation of the distribution (and also its median and mode), while the parameter σ is its standard deviation. The variance of the distribution is σ^2. A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate.

Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable whose distribution converges to a normal distribution as the number of samples increases. Therefore, physical quantities that are expected to be the sum of many independent processes, such as measurement errors, often have distributions that are nearly normal.

A normal distribution is sometimes informally called a bell curve. However, many other distributions are bell-shaped (such as the Cauchy, Student’s t, and logistic distributions).

Importance of Normal Distribution:

  1. Foundation of Statistical Inference

The normal distribution is central to statistical inference. Many parametric tests, such as t-tests and ANOVA, are based on the assumption that the data follows a normal distribution. This simplifies hypothesis testing, confidence interval estimation, and other analytical procedures.

  1. Real-Life Data Approximation

Many natural phenomena and datasets, such as heights, weights, IQ scores, and measurement errors, tend to follow a normal distribution. This makes it a practical and realistic model for analyzing real-world data, simplifying interpretation and analysis.

  1. Basis for Central Limit Theorem (CLT)

The normal distribution is critical in understanding the Central Limit Theorem, which states that the sampling distribution of the sample mean approaches a normal distribution as the sample size increases, regardless of the population’s actual distribution. This enables statisticians to make predictions and draw conclusions from sample data.

  1. Application in Quality Control

In industries, normal distribution is widely used in quality control and process optimization. Control charts and Six Sigma methodologies assume normality to monitor processes and identify deviations or defects effectively.

  1. Probability Calculations

The normal distribution allows for the easy calculation of probabilities for different scenarios. Its standardized form, the z-score, simplifies these calculations, making it easier to determine how data points relate to the overall distribution.

  1. Modeling Financial and Economic Data

In finance and economics, normal distribution is used to model returns, risks, and forecasts. Although real-world data often exhibit deviations, normal distribution serves as a baseline for constructing more complex models.

Central limit theorem

In probability theory, the central limit theorem (CLT) establishes that, in many situations, when independent random variables are added, their properly normalized sum tends toward a normal distribution (informally a bell curve) even if the original variables themselves are not normally distributed. The theorem is a key concept in probability theory because it implies that probabilistic and statistical methods that work for normal distributions can be applicable to many problems involving other types of distributions. This theorem has seen many changes during the formal development of probability theory. Previous versions of the theorem date back to 1810, but in its modern general form, this fundamental result in probability theory was precisely stated as late as 1920, thereby serving as a bridge between classical and modern probability theory.

Characteristics Fitting a Normal Distribution

Management Notes

Poisson Distribution: Importance Conditions Constants, Fitting of Poisson Distribution

indiafreenotesby indiafreenotes1

Poisson distribution is a probability distribution used to model the number of events occurring within a fixed interval of time, space, or other dimensions, given that these events occur independently and at a constant average rate.

Importance

  1. Modeling Rare Events: Used to model the probability of rare events, such as accidents, machine failures, or phone call arrivals.
  2. Applications in Various Fields: Applicable in business, biology, telecommunications, and reliability engineering.
  3. Simplifies Complex Processes: Helps analyze situations with numerous trials and low probability of success per trial.
  4. Foundation for Queuing Theory: Forms the basis for queuing models used in service and manufacturing industries.
  5. Approximation of Binomial Distribution: When the number of trials is large, and the probability of success is small, Poisson distribution approximates the binomial distribution.

Conditions for Poisson Distribution

  1. Independence: Events must occur independently of each other.
  2. Constant Rate: The average rate (λ) of occurrence is constant over time or space.
  3. Non-Simultaneous Events: Two events cannot occur simultaneously within the defined interval.
  4. Fixed Interval: The observation is within a fixed time, space, or other defined intervals.

Constants

  1. Mean (λ): Represents the expected number of events in the interval.
  2. Variance (λ): Equal to the mean, reflecting the distribution’s spread.
  3. Skewness: The distribution is skewed to the right when λ is small and becomes symmetric as λ increases.
  4. Probability Mass Function (PMF): P(X = k) = [e^−λ*λ^k] / k!, Where is the number of occurrences, is the base of the natural logarithm, and λ is the mean.

Fitting of Poisson Distribution

When a Poisson distribution is to be fitted to an observed data the following procedure is adopted:

Management Notes

Binomial Distribution: Importance Conditions, Constants

indiafreenotesby indiafreenotes1

The binomial distribution is a probability distribution that summarizes the likelihood that a value will take one of two independent values under a given set of parameters or assumptions. The underlying assumptions of the binomial distribution are that there is only one outcome for each trial, that each trial has the same probability of success, and that each trial is mutually exclusive, or independent of each other.

In probability theory and statistics, the binomial distribution with parameters n and p is the discrete probability distribution of the number of successes in a sequence of n independent experiments, each asking a yes, no question, and each with its own Boolean-valued outcome: success (with probability p) or failure (with probability q = 1 − p). A single success/failure experiment is also called a Bernoulli trial or Bernoulli experiment, and a sequence of outcomes is called a Bernoulli process; for a single trial, i.e., n = 1, the binomial distribution is a Bernoulli distribution. The binomial distribution is the basis for the popular binomial test of statistical significance.

The binomial distribution is frequently used to model the number of successes in a sample of size n drawn with replacement from a population of size N. If the sampling is carried out without replacement, the draws are not independent and so the resulting distribution is a hypergeometric distribution, not a binomial one. However, for N much larger than n, the binomial distribution remains a good approximation, and is widely used

The binomial distribution is a common discrete distribution used in statistics, as opposed to a continuous distribution, such as the normal distribution. This is because the binomial distribution only counts two states, typically represented as 1 (for a success) or 0 (for a failure) given a number of trials in the data. The binomial distribution, therefore, represents the probability for x successes in n trials, given a success probability p for each trial.

Binomial distribution summarizes the number of trials, or observations when each trial has the same probability of attaining one particular value. The binomial distribution determines the probability of observing a specified number of successful outcomes in a specified number of trials.

The binomial distribution is often used in social science statistics as a building block for models for dichotomous outcome variables, like whether a Republican or Democrat will win an upcoming election or whether an individual will die within a specified period of time, etc.

Importance

For example, adults with allergies might report relief with medication or not, children with a bacterial infection might respond to antibiotic therapy or not, adults who suffer a myocardial infarction might survive the heart attack or not, a medical device such as a coronary stent might be successfully implanted or not. These are just a few examples of applications or processes in which the outcome of interest has two possible values (i.e., it is dichotomous). The two outcomes are often labeled “success” and “failure” with success indicating the presence of the outcome of interest. Note, however, that for many medical and public health questions the outcome or event of interest is the occurrence of disease, which is obviously not really a success. Nevertheless, this terminology is typically used when discussing the binomial distribution model. As a result, whenever using the binomial distribution, we must clearly specify which outcome is the “success” and which is the “failure”.

The binomial distribution model allows us to compute the probability of observing a specified number of “successes” when the process is repeated a specific number of times (e.g., in a set of patients) and the outcome for a given patient is either a success or a failure. We must first introduce some notation which is necessary for the binomial distribution model.

First, we let “n” denote the number of observations or the number of times the process is repeated, and “x” denotes the number of “successes” or events of interest occurring during “n” observations. The probability of “success” or occurrence of the outcome of interest is indicated by “p”.

The binomial equation also uses factorials. In mathematics, the factorial of a non-negative integer k is denoted by k!, which is the product of all positive integers less than or equal to k. For example,

  • 4! = 4 x 3 x 2 x 1 = 24,
  • 2! = 2 x 1 = 2,
  • 1!=1.
  • There is one special case, 0! = 1.

Conditions

  • The number of observations n is fixed.
  • Each observation is independent.
  • Each observation represents one of two outcomes (“success” or “failure”).
  • The probability of “success” p is the same for each outcome

Constants

Fitting of Binomial Distribution

Fitting of probability distribution to a series of observed data helps to predict the probability or to forecast the frequency of occurrence of the required variable in a certain desired interval.

To fit any theoretical distribution, one should know its parameters and probability distribution. Parameters of Binomial distribution are n and p. Once p and n are known, binomial probabilities for different random events and the corresponding expected frequencies can be computed. From the given data we can get n by inspection. For binomial distribution, we know that mean is equal to np hence we can estimate p as = mean/n. Thus, with these n and p one can fit the binomial distribution.

There are many probability distributions of which some can be fitted more closely to the observed frequency of the data than others, depending on the characteristics of the variables. Therefore, one needs to select a distribution that suits the data well.

Management Notes

Calculation of Interest

indiafreenotesby indiafreenotes3

Calculating interest rate is not at all a difficult method to understand. Knowing to calculate interest rate can solve a lot of wages problems and save money while taking investment decisions. There is an easy formula to calculate simple interest rates. If you are aware of your loan and interest amount you can pay, you can do the largest interest rate calculation for yourself.

Using the simple interest calculation formula, you can also see your interest payments in a year and calculate your annual percentage rate.

Here is the step by step guide to calculate the interest rate.

How to calculate interest rate?

Know the formula which can help you to calculate your interest rate.

Step 1

To calculate your interest rate, you need to know the interest formula I/Pt = r to get your rate. Here,

I = Interest amount paid in a specific time period (month, year etc.)

P = Principle amount (the money before interest)

t = Time period involved

r = Interest rate in decimal

You should remember this equation to calculate your basic interest rate.

Step 2

Once you put all the values required to calculate your interest rate, you will get your interest rate in decimal. Now, you need to convert the interest rate you got by multiplying it by 100. For example, a decimal like .11 will not help much while figuring out your interest rate. So, if you want to find your interest rate for .11, you have to multiply .11 with 100 (.11 x 100).

For this case, your interest rate will be (.11 x 100 = 11) 11%.

Step 3

Apart from this, you can also calculate your time period involved, principal amount and interest amount paid in a specific time period if you have other inputs available with you.

Calculate interest amount paid in a specific time period, I = Prt.

Calculate the principal amount, P = I/rt.

Calculate time period involved t = I/Pr.

Step 4

Most importantly, you have to make sure that your time period and interest rate are following the same parameter.

For example, on a loan, you want to find your monthly interest rate after one year. In this case, if you put t = 1, you will get the final interest rate as the interest rate per year. Whereas, if you want the monthly interest rate, you have to put the correct amount of time elapsed. Here, you can consider the time period like 12 months.

Please remember, your time period should be the same time amount as the interest paid. For example, if you’re calculating a year’s monthly interest payments then, it can be considered you’ve made 12 payments.

Also, you have to make sure that you check the time period (weekly, monthly, yearly etc.) when your interest is calculated with your bank.

Step 5

You can rely on online calculators to get interest rates for complex loans, such as mortgages. You should also know the interest rate of your loan when you sign up for it.

For fluctuating rates, sometimes it becomes difficult to determine what a certain rate means. So, it is better to use free online calculators by searching “variable APR interest calculator”, “mortgage interest calculator” etc.

Calculation of interest when rate of interest and cash price is given

  • Where Cash Price, Interest Rate and Instalment are Given:

Illustration:

On 1st January 2003, A bought a television from a seller under Hire Purchase System, the cash price of which being Rs 10.450 as per the following terms:

(a) Rs 3,000 to be paid on signing the agreement.

(b) Balance to be paid in three equal installments of Rs 3,000 at the end of each year,

(c) The rate of interest charged by the seller is 10% per annum.

You are required to calculate the interest paid by the buyer to the seller each year.

Solution:

Note:

  1. there is no time gap between the signing of the agreement and the cash down payment of Rs 3,000 (1.1.2003). Hence no interest is calculated. The entire amount goes to reduce the cash price.
  2. The interest in the last installment is taken at the differential figure of Rs 285.50 (3,000 – 2,714.50).

(2) Where Cash Price and Installments are Given but Rate of Interest is Omitted:

Where the rate of interest is not given and only the cash price and the total payments under hire purchase installments are given, then the total interest paid is the difference between the cash price of the asset and the total amount paid as per the agreement. This interest amount is apportioned in the ratio of amount outstanding at the end of each period.

Illustration:

Mr. A bought a machine under hire purchase agreement, the cash price of the machine being Rs 18,000. As per the terms, the buyer has to pay Rs 4,000 on signing the agreement and the balance in four installments of Rs 4,000 each, payable at the end of each year. Calculate the interest chargeable at the end of each year.

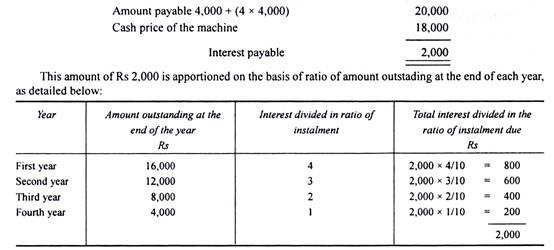
(3) Where installments and Rate of Interest are Given but Cash Value of the Asset is Omitted:

In certain problems, the cash price is not given. It is necessary that we must first find out the cash price and interest included in the installments. The asset account is to be debited with the actual price of the asset. Under such situations, i.e. in the absence of cash price, the interest is calculated from the last year.

It may be noted that the amount of interest goes on increasing from 3rd year to 2nd year, 2nd year to 1st year. Since the interest is included in the installments and by knowing the rate of interest, we can find out the cash price.

Thus:

Let the cash price outstanding be: Rs 100

Interest @ 10% on Rs 100 for a year: Rs 10

Installment paid at the end of the year 110

The interest on installment price = 10/110 or 1/11 as a ratio.

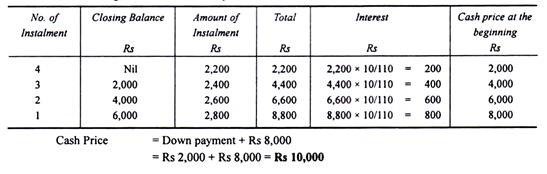
Illustration:

I buy a television on Hire Purchase System.

The terms of payment are as follows:

Rs 2,000 to be paid on signing the agreement;

Rs 2,800 at the end of the first year;

Rs 2,600 at the end of the second year;

Rs 2,400 at the end of the third year;

Rs 2,200 at the end of the fourth year.

If interest is charged at the rate of 10% p.a., what was the cash value of the television?

Solution:

(4) Calculation of Cash Price when Reference to Annuity Table, the Rate of Interest and Installments are Given:

Sometimes in the problem a reference to annuity table wherein present value of the annuity for a number of years at a certain rate of interest is given. In such cases the cash price is calculated by multiplying the amount of installment and adding the product to the initial payment.

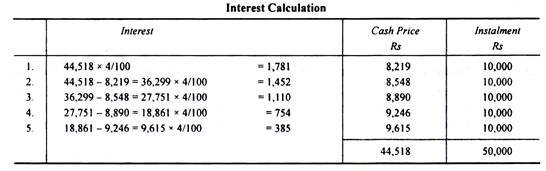
Illustration:

A agrees to purchase a machine from a seller under Hire Purchase System by annual installment of Rs 10,000 over a period of 5 years. The seller charges interest at 4% p.a. on yearly balance.

N.B. The present value of Re 1 p.a. for five years at 4% is Rs 4.4518. Find out the cash price of the machine.

Solution:

Installment Re 1 Present value = Rs 4.4518

Installment = Rs 10,000 Present value = Rs 4.4518 x 10,000 = Rs 44,518

Credit: https://www.yourarticlelibrary.com/accounting/hire-purchase/how-to-calculate-interest-4-cases-hire-purchase/51175

Bangalore University BBA Notes

Quantitative Methods for Business – 1

indiafreenotesby indiafreenotes1

Unit 1 Number System {Book}

Natural Numbers, Even Numbers, Odd Numbers

VIEW

Integers, Prime Numbers

VIEW

Rational & Irrational numbers

VIEW

Real Numbers, HCF & LCM (Simple Problems)

VIEW

Unit 2 Theory Of Equations {Book}

Please refer Books for this Unit

VIEW

Unit 3 Progressions {Book}

Arithmetic Progression Finding the “n”th term of AP and Sum to “n”th term of AP.

VIEW

Insertion of Arithmetic Mean

VIEW

Geometric Progression Finding the “n”th term of GP and

VIEW

Insertion of Geometric Mean

VIEW

Unit 4 Matrices and Determinants {Book}

Please refer Books for this Unit

VIEW

Unit 4 Commercial Arithmetic {Book}

Simple Interest, Compound Interest including half yearly and quarterly calculations

VIEW

Annuities

VIEW

Percentages

VIEW

Bills Discounting

VIEW

Ratios and proportions

VIEW

Duplicate: Triplicate and Sub-duplicate of a ratio

VIEW

Proportions: Third, Fourth and inverse proportion

VIEW

Unit 5 Progressions {Book}

Arithmetic Progression Finding the “n”th term of AP and Sum to “n”th term of AP.

VIEW

Insertion of Arithmetic Mean

VIEW

Geometric Progression Finding the “n”th term of GP and

VIEW

Insertion of Geometric Mean

VIEW

error: Content is protected !!