Mean (AM, Weighted, Combined)

AM

The arithmetic mean,’ mean or average is calculated by summ­ing all the individual observations or items of a sample and divid­ing this sum by the number of items in the sample. For example, as the result of a gas analysis in a respirometer an investigator obtains the following four readings of oxygen percentages:

14.9

10.8

12.3

23.3

Sum = 61.3

He calculates the mean oxygen percentage as the sum of the four items divided by the number of items here, by four. Thus, the average oxygen percentage is

Mean = 61.3 / 4 =15.325%

Calculating a mean presents us with the opportunity for learning statistical symbolism. An individual observation is symbo­lized by Y_i, which stands for the ith observation in the sample. Four observations could be written symbolically as Yi, Y₂, Y₃, Y₄.

We shall define n, the sample size, as the number of items in a sample. In this particular instance, the sample size n is 4. Thus, in a large sample, we can symbolize the array from the first to the nth item as follows: Y₁, Y₂…, Y_n. When we wish to sum items, we use the following notation:

The capital Greek sigma, Ʃ, simply means the sum of items indica­ted. The i = 1 means that the items should be summed, starting with the first one, and ending with the nth one as indicated by the i = n above the Ʃ. The subscript and superscript are necessary to indicate how many items should be summed. Below are seen increasing simplifications of the complete notation shown at the extreme left:

Properties of Arithmetic Mean:

1. The sum of deviations of the items from the arithmetic mean is always zero i.e.

∑(X–X) =0.

2. The Sum of the squared deviations of the items from A.M. is minimum, which is less than the sum of the squared deviations of the items from any other values.
3. If each item in the series is replaced by the mean, then the sum of these substitutions will be equal to the sum of the individual items.                       

Merits of A.M:

1. It is simple to understand and easy to calculate.
2. It is affected by the value of every item in the series.
3. It is rigidly defined.
4. It is capable of further algebraic treatment.
5. It is calculated value and not based on the position in the series.

Demerits of A.M:

1. It is affected by extreme items i.e., very small and very large items.
2. It can hardly be located by inspection.
3. In some cases A.M. does not represent the actual item. For example, average patients admitted in a hospital is 10.7 per day.
4. M. is not suitable in extremely asymmetrical distributions.

Weighted

In some cases, you might want a number to have more weight. In that case, you’ll want to find the weighted mean. To find the weighted mean:

1. Multiply the numbers in your data set by the weights.
2. Add the results up.

For that set of number above with equal weights (1/5 for each number), the math to find the weighted mean would be:
1(*1/5) + 3(*1/5) + 5(*1/5) + 7(*1/5) + 10(*1/5) = 5.2.

Sample problem: You take three 100-point exams in your statistics class and score 80, 80 and 95. The last exam is much easier than the first two, so your professor has given it less weight. The weights for the three exams are:

• Exam 1: 40 % of your grade. (Note: 40% as a decimal is .4.)
• Exam 2: 40 % of your grade.
• Exam 3: 20 % of your grade.

What is your final weighted average for the class?

1. Multiply the numbers in your data set by the weights:
   .4(80) = 32
   .4(80) = 32
   .2(95) = 19
2. Add the numbers up. 32 + 32 + 19 = 83.

The percent weight given to each exam is called a weighting factor.

Weighted Mean Formula

The weighted mean is relatively easy to find. But in some cases the weights might not add up to 1. In those cases, you’ll need to use the weighted mean formula. The only difference between the formula and the steps above is that you divide by the sum of all the weights.

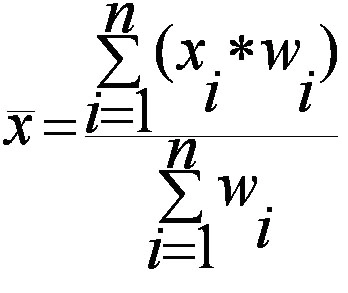
The image above is the technical formula for the weighted mean. In simple terms, the formula can be written as:
Weighted mean = Σwx/Σw
Σ = the sum of (in other words…add them up!).
w = the weights.
x = the value.

To use the formula:

1. Multiply the numbers in your data set by the weights.
2. Add the numbers in Step 1 up. Set this number aside for a moment.
3. Add up all of the weights.
4. Divide the numbers you found in Step 2 by the number you found in Step 3.

In the sample grades problem above, all of the weights add up to 1 (.4 + .4 + .2) so you would divide your answer (83) by 1:
83 / 1 = 83.

However, let’s say your weighted means added up to 1.2 instead of 1. You’d divide 83 by 1.2 to get:
83 / 1.2 = 69.17.

Combined Mean

A combined mean is a mean of two or more separate groups, and is found by:

1. Calculating the mean of each group,
2. Combining the results.

Combined Mean Formula

More formally, a combined mean for two sets can be calculated by the formula :

Where:

• x_a = the mean of the first set,
• m = the number of items in the first set,
• x_b = the mean of the second set,
• n = the number of items in the second set,
• x_c the combined mean.

A combined mean is simply a weighted mean, where the weights are the size of each group.