Absolute skewness
This is obtained by finding the difference between any two measures of dispersion viz: Mean, Median and More. Thus, Skewness or
| Sk = | X –M | or X – Z | or M-Z |
Any positive value obtained by any of the above formulae is marked as the extent of the positive skewness. Any negative value obtained by any of the above formulae is marked as the extent of the negative skewness of the distribution. If the result produced is zero, it signifies the absence of skewness in the distribution.
(a) Co-efficient of skewness
This is obtained by dividing the Skewness by any measure of dispersion.
Thus,
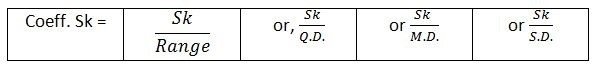
Karl Pearson’s Skewness
Prof. Karl pearson says that to study the skewness of a series, the difference between the Mean and Mode only should be found out. This is because, Mean is an average which is affected very much by the extreme values of a series and Mode is an average which is least affected by the extreme values of a series. Thus, according to him,
Sk(p) = Mean –Mode
When, Mode is ill defined i.e. when it has different values, Prof. Pearson proposes to find out the skewness by the following formula:
Sk(p) = 3 (Mean –Median)
This formula is based on the empirical relationship between Mean, Median and Mode which is as follows:
Absolute Mode= 3 Median – 2 Mean
Thus, Sk(p) = X¯ – (3M- 2X¯)
= X¯ – 3M +2X¯
= 3X¯ – 3M
= 3(X¯ -M)
For finding the coefficient of skewness, Prof. Pearson advocates that only standard diviation should be taken as the divisor of the absolute skewness. This is because, standard deviation is the only measure of dispersion which possesses many algebraic properties, and other measures of dispersion are not capable of algebraic treatments. Thus, his coefficient of skewness is given by:

Limits of the results
Prof. Pearson claims that the results of his coefficient of skewness shall lie withing ± 3.
Bowley’s Skewness
According to Prof. A.L. Bowley, the presence, or absence of skewness will be determined on the basis of the distance of the quartiles from the Median. Thus, his skewness is given by
SK(B) = (Q3 – M) – (M –Q1)
Or = Q3 + Q1 -2M
If the above equation results in zero, it will indicate the absence of skewness or symmetricity of the distribution. On the other hand, if the said equation results in some positive, or negative figure, the same will be marked as the extent of the positive, or negative skewness of the series respectively.
Further, the coefficient, the coefficient of skewness of Prof. Bowley is given by:
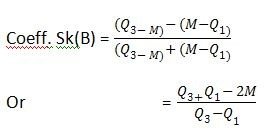
2 thoughts on “Absolute and Relative skewness measures, Karl Pearson’s Co-efficient of Skewness, Bowley’s Co-efficient of Skewness”