Sinking Fund, Purpose, Structure, Benefits, Applications
Sinking Fund is a financial mechanism used to set aside money over time for the purpose of repaying debt or replacing a significant asset. It acts as a savings plan that allows an organization or individual to accumulate funds for a specific future obligation, ensuring that they have enough resources to meet that obligation without straining their financial situation.
Purpose of a Sinking Fund:
The primary purpose of a sinking fund is to manage debt repayment or asset replacement efficiently.
-
Reduce Default Risk:
By setting aside funds regularly, borrowers can reduce the risk of default on their obligations. This practice assures lenders that the borrower is financially responsible and prepared to meet repayment terms.
-
Facilitate Large Purchases:
For organizations, sinking funds can help manage significant future expenditures, such as replacing machinery, vehicles, or technology. This ensures that funds are available when needed, mitigating the impact on cash flow.
-
Enhance Financial Planning:
Establishing a sinking fund encourages better financial planning and discipline. Organizations can forecast their future cash requirements, making it easier to allocate resources appropriately.
Structure of a Sinking Fund:
-
Regular Contributions:
The entity responsible for the sinking fund makes regular contributions, typically monthly or annually. The amount of these contributions can be fixed or variable based on a predetermined plan.
-
Interest Earnings:
The contributions are usually invested in low-risk securities or interest-bearing accounts. This investment allows the sinking fund to grow over time through interest earnings, ultimately increasing the amount available for future obligations.
- Target Amount:
The sinking fund is established with a specific target amount that reflects the total debt or asset replacement cost. The time frame for reaching this target is also defined, ensuring that contributions align with the due date for the obligation.
Benefits of a Sinking Fund:
-
Financial Stability:
By accumulating funds over time, sinking funds contribute to financial stability, reducing the pressure to secure large amounts of money at once.
-
Improved Creditworthiness:
A well-managed sinking fund can enhance an organization’s credit rating. Lenders view sinking funds as a positive indicator of an entity’s ability to manage its debts responsibly.
-
Cost Management:
Sinking funds help manage the cost of large purchases or debt repayments by spreading the financial burden over time, reducing the impact on cash flow.
- Flexibility:
The structure of a sinking fund can be adjusted based on changing financial circumstances. Contributions can be increased or decreased as needed, providing flexibility in financial planning.
-
Risk Mitigation:
By setting aside funds in advance, entities can mitigate the risks associated with sudden financial obligations, ensuring they are prepared for unexpected expenses or economic downturns.
Practical Applications of Sinking Funds:
-
Corporate Bonds:
Many corporations issue bonds that require a sinking fund to be established. The company sets aside money regularly to repay bondholders at maturity or periodically throughout the life of the bond.
-
Municipal Bonds:
Local governments often use sinking funds to repay municipal bonds. This practice ensures that they can meet their obligations without significantly impacting their budgets.
-
Asset Replacement:
Businesses may establish sinking funds for replacing equipment or vehicles. By planning ahead, they can avoid large capital outlays and maintain operations without disruption.
-
Real Estate:
Property management companies may set up sinking funds for the maintenance and eventual replacement of common areas or amenities within residential complexes.
-
Educational Institutions:
Schools and universities may use sinking funds to save for future building projects or major renovations, ensuring they can finance these endeavors without resorting to debt.



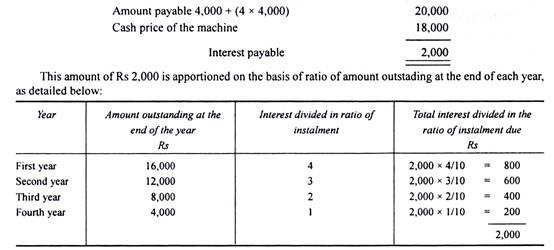
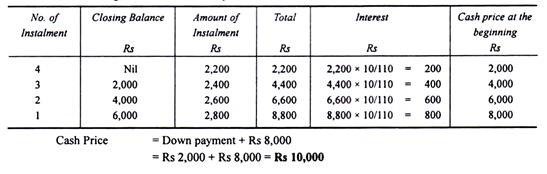
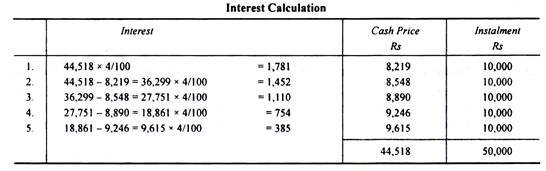


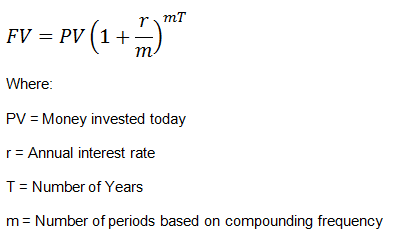
 Example:
Example: