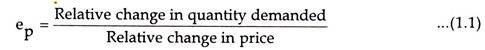Demand forecasting is the process of estimating the future demand for a product or service over a specific period. It is a critical component of business planning that helps organizations make informed decisions regarding production, inventory management, pricing, marketing, and resource allocation. Accurate demand forecasting enables businesses to anticipate customer needs, avoid overproduction or underproduction, and optimize operational efficiency.
The goal of demand forecasting is to reduce uncertainty and support strategic planning by predicting how much of a product consumers will be willing and able to purchase in the future. Forecasts are based on a combination of historical sales data, market trends, seasonal patterns, consumer behaviour, and external economic indicators. Businesses may use qualitative methods (like expert opinion and market research) or quantitative methods (like time series analysis, regression models, and machine learning algorithms) depending on the context and available data.
There are different types of demand forecasting, such as short-term forecasting (used for inventory and scheduling), medium-term forecasting (for sales and budget planning), and long-term forecasting (for capacity and expansion decisions). Each serves a specific business purpose.
Effective demand forecasting provides several benefits. It helps reduce costs, improves customer satisfaction through better availability of products, and enhances financial planning by aligning supply with anticipated demand. It also minimizes the risks of stockouts or surplus inventory.
In today’s competitive and dynamic market environment, demand forecasting is essential for gaining a competitive edge, ensuring customer satisfaction, and achieving overall business success. It supports data-driven decision-making and enables organizations to respond proactively to market changes.
Need of Demand Forecasting:
Demand plays a crucial role in the management of every business. It helps an organization to reduce risks involved in business activities and make important business decisions. Apart from this, demand forecasting provides an insight into the organization’s capital investment and expansion decisions.
- Business Planning and Strategy
Demand forecasting is essential for long-term business planning and the formulation of strategies. It helps managers estimate future demand and align their production, investment, and marketing efforts accordingly. Forecasting provides insights into market trends, consumer behavior, and potential changes in demand patterns. This enables firms to develop strategies that minimize risks and capitalize on growth opportunities. Accurate forecasts guide business decisions regarding expansion, diversification, and resource allocation, thereby supporting sustainable growth and competitive advantage in dynamic business environments.
- Production Planning and Scheduling
Forecasting demand enables businesses to plan production activities efficiently. It helps determine the quantity of raw materials, machinery, and labor required to meet expected demand. Proper production planning ensures timely delivery of goods, minimizes lead times, and avoids production bottlenecks. It also helps in reducing production costs by optimizing resource utilization. With accurate demand projections, companies can avoid overproduction, which leads to excess inventory, or underproduction, which causes stockouts and customer dissatisfaction. Thus, forecasting is crucial for streamlined operations.
- Financial Planning and Budgeting
Demand forecasting plays a critical role in financial planning. It helps businesses estimate future revenues and costs, which is vital for preparing budgets, managing cash flows, and assessing profitability. Accurate forecasts allow firms to anticipate financial needs, allocate funds appropriately, and plan for future investments. It also aids in obtaining credit and financial support, as lenders often require evidence of projected demand and income. In essence, demand forecasting supports better fiscal discipline and long-term financial health of an organization.
Proper demand forecasting ensures effective inventory management. By predicting the demand accurately, businesses can maintain optimum stock levels — not too high to incur carrying costs, and not too low to miss sales opportunities. It prevents situations of excess inventory that can lead to wastage, especially for perishable goods, and also avoids stockouts that frustrate customers. Forecasting aligns inventory control with market demand, thus ensuring product availability while keeping storage costs and capital investment in inventory at manageable levels.
Accurate demand forecasts help determine labor requirements for upcoming production and sales activities. Businesses can estimate the number and types of employees needed during peak and off-peak seasons. For example, retailers hire more staff during festive seasons based on expected demand. This ensures optimal workforce allocation, better scheduling, and reduced employee downtime. Demand forecasting thus supports human resource planning by aligning labor supply with demand, ensuring that operations are smooth, cost-effective, and responsive to customer needs.
- Marketing and Promotional Strategy
Forecasting demand is crucial for developing effective marketing campaigns and promotional activities. By knowing when and where demand is likely to rise, companies can focus their marketing efforts strategically. It enables them to allocate budgets, select appropriate channels, and time promotions to boost sales. For example, a forecasted surge in demand during holidays helps firms plan discounts or advertising campaigns in advance. In this way, demand forecasting improves marketing ROI and strengthens customer engagement and brand positioning.
Demand forecasting provides critical input for pricing decisions. Understanding demand elasticity helps firms decide whether to raise or lower prices to maximize revenue. If forecasts show high future demand, businesses may maintain or increase prices. In contrast, if demand is expected to fall, they may consider promotional pricing or discounts. Accurate forecasting allows for dynamic pricing strategies that align with market conditions and consumer expectations, helping businesses stay competitive while optimizing profit margins.
- Risk Management and Crisis Preparation
One of the most important needs of demand forecasting is to manage business risks. Forecasts allow firms to anticipate shifts in demand due to economic changes, competitor actions, or consumer preferences. This preparation helps companies develop contingency plans, adjust operations, and adapt their offerings accordingly. For instance, during uncertain periods like pandemics or economic slowdowns, forecasting enables proactive decision-making. It enhances organizational resilience by reducing uncertainty and enabling firms to react swiftly to market disruptions.
Objectives of short term demand forecasting:
Short-term demand forecasting helps businesses maintain optimal inventory levels. By predicting near-future demand, firms avoid understocking or overstocking, which reduces storage costs and prevents stockouts. It ensures that inventory is aligned with expected sales, thereby improving customer satisfaction and operational efficiency. Effective inventory planning also minimizes losses due to obsolescence or spoilage, especially for perishable or seasonal products.
Short-term forecasts are crucial for daily or weekly production scheduling. They allow businesses to adjust their production volume based on immediate market demand. This prevents overproduction, reduces idle time, and ensures efficient use of resources. Production planning based on accurate short-term forecasts also helps maintain quality control and timely delivery, which are essential for meeting customer expectations and reducing operational costs.
Forecasting short-term demand allows businesses to align their workforce requirements with production and service needs. Companies can schedule shifts, plan overtime, or hire temporary workers during peak periods. It ensures optimal manpower utilization and prevents labor shortages or surpluses. This leads to cost-effective operations and maintains employee satisfaction by avoiding overburdening during high-demand periods or underemployment during low-demand phases.
Short-term demand forecasting helps in making timely pricing decisions. If a surge in demand is anticipated, businesses may increase prices to maximize profits. Conversely, during a slowdown, they might offer discounts or promotions to stimulate demand. This flexibility in pricing ensures competitiveness, helps clear inventory, and supports revenue targets. Effective pricing adjustments based on demand help maintain a stable market position.
Forecasting demand over the short term helps businesses time their marketing and promotional activities for maximum impact. If demand is expected to rise, promotional efforts can be intensified to boost brand visibility. During slow periods, targeted campaigns can help stimulate customer interest. Proper timing of promotions improves return on marketing investment and ensures better alignment between marketing strategy and consumer behavior.
Short-term forecasting supports accurate cash flow and budget planning. By estimating near-future sales and expenses, firms can manage working capital, schedule purchases, and plan for short-term financing needs. It reduces the likelihood of liquidity issues and ensures smooth operations. Financial planning based on short-term forecasts allows for timely payment of obligations, better credit management, and informed decision-making regarding short-term investments.
- Customer Service Management
Short-term demand forecasting ensures products and services are available when customers need them. This helps improve order fulfillment rates, reduce waiting times, and enhance customer satisfaction. Meeting customer demand promptly builds trust and loyalty. It also enables businesses to handle sudden demand spikes efficiently, ensuring they remain responsive and competitive in fast-moving markets.
- Managing Seasonal and Promotional Demand
Short-term forecasts are essential for anticipating seasonal variations and promotional event impacts. For example, demand often spikes during festivals or clearance sales. Accurate forecasting allows companies to prepare in advance, stocking up on popular products and aligning logistics accordingly. This minimizes disruption, boosts sales, and ensures timely service delivery during high-demand periods.
Objectives of long term demand forecasting:
- Strategic Business Planning
Long-term demand forecasting provides the foundation for strategic decision-making. It helps businesses plan future goals, set long-term objectives, and align operations with projected market trends. Accurate forecasts enable companies to anticipate industry changes, customer needs, and competitive pressures, helping them maintain a sustainable competitive advantage. It supports decisions related to diversification, globalization, and product innovation over extended time horizons.
- Capital Investment Decisions
Businesses rely on long-term demand forecasting to plan for capital investments such as new plants, machinery, technology upgrades, or infrastructure development. These decisions require large financial commitments and long gestation periods. Forecasting helps determine whether anticipated demand justifies such investments. It ensures that resources are not wasted on underutilized assets and enables the organization to plan investments that support future capacity needs.
To meet future demand effectively, firms need to plan their production and operational capacity well in advance. Long-term forecasting helps determine when and how much to expand capacity. It guides decisions about scaling production lines, adding shifts, or establishing new facilities. This ensures businesses are prepared to meet future demand increases without facing operational bottlenecks or sacrificing customer service quality.
- Research and Development (R&D) Planning
Long-term forecasts inform decisions regarding research and development. Businesses can identify future market needs and begin working on new products or improving existing ones. This planning ensures that companies are not reactive but proactive, launching innovative solutions at the right time. R&D planning based on demand projections helps businesses remain technologically advanced and responsive to evolving consumer preferences.
- Human Resource Development
Long-term forecasting supports workforce planning and development strategies. It helps organizations estimate future staffing needs, plan recruitment drives, invest in employee training, and develop succession plans. This ensures that the business has the right talent and skills available when needed. Preparing a future-ready workforce reduces the risk of talent shortages and helps organizations stay competitive and productive in the long run.
- Financial Forecasting and Capital Allocation
Forecasting long-term demand assists in financial forecasting and efficient capital allocation. It helps determine future revenue streams, investment priorities, and funding requirements. Businesses can prepare long-term budgets, secure financing in advance, and allocate capital to areas with the highest expected returns. Long-term financial stability is strengthened when capital planning aligns with realistic demand estimates.
- Risk Management and Contingency Planning
Long-term demand forecasting allows businesses to identify potential risks, such as market downturns, raw material shortages, or technological disruptions. Companies can then create contingency plans to mitigate these risks in advance. This proactive approach enhances organizational resilience, supports crisis readiness, and enables smoother operations even in uncertain or volatile environments.
- Expansion and Diversification Strategy
Businesses aiming to grow through market expansion or diversification use long-term demand forecasting to identify viable opportunities. Forecasts indicate potential markets, emerging customer segments, and product demand trends. These insights support decisions on entering new geographic areas, launching new product lines, or acquiring complementary businesses. Long-term planning ensures resources are directed toward sustainable growth areas.
Methods of Demand Forecasting:
There is no easy or simple formula to forecast the demand. Proper judgment along with the scientific formula is needed to correctly predict the future demand for a product or service. Some methods of demand forecasting are discussed below:
1. Survey of Buyer’s Choice
When the demand needs to be forecasted in the short run, say a year, then the most feasible method is to ask the customers directly that what are they intending to buy in the forthcoming time period. Thus, under this method, the potential customers are directly interviewed. This survey can be done in any of the following ways:
- Complete Enumeration Method: Under this method, nearly all the potential buyers are asked about their future purchase plans.
- Sample Survey Method: Under this method, a sample of potential buyers is chosen scientifically and only those chosen are interviewed.
- End-use Method: It is especially used for forecasting the demand of the inputs. Under this method, the final users i.e. the consuming industries and other sectors are identified. The desirable norms of consumption of the product are fixed, the targeted output levels are estimated and these norms are applied to forecast the future demand of the inputs.
Hence, it can be said that under this method the burden of demand forecasting is on the buyer. However, the judgments of the buyers are not completely reliable and so the seller should take decisions in the light of his judgment also.
The customer may misjudge their demands and may also change their decisions in the future which in turn may mislead the survey. This method is suitable when goods are supplied in bulk to industries but not in the case of household customers.
2. Collective Opinion Method
Under this method, the salesperson of a firm predicts the estimated future sales in their region. The individual estimates are aggregated to calculate the total estimated future sales. These estimates are reviewed in the light of factors like future changes in the selling price, product designs, changes in competition, advertisement campaigns, the purchasing power of the consumers, employment opportunities, population, etc.
The principle underlying this method is that as the salesmen are closest to the consumers they are more likely to understand the changes in their needs and demands. They can also easily find out the reasons behind the change in their tastes.
Therefore, a firm having good sales personnel can utilize their experience to predict the demands. Hence, this method is also known as Salesforce opinion or Grassroots approach method. However, this method depends on the personal opinions of the sales personnel and is not purely scientific.
3. Barometric Method
This method is based on the past demands of the product and tries to project the past into the future. The economic indicators are used to predict the future trends of the business. Based on the future trends, the demand for the product is forecasted. An index of economic indicators is formed. There are three types of economic indicators, viz. leading indicators, lagging indicators, and coincidental indicators.
The leading indicators are those that move up or down ahead of some other series. The lagging indicators are those that follow a change after some time lag. The coincidental indicators are those that move up and down simultaneously with the level of economic activities.
4. Market Experiment Method
Another one of the methods of demand forecasting is the market experiment method. Under this method, the demand is forecasted by conducting market studies and experiments on consumer behavior under actual but controlled, market conditions.
Certain determinants of demand that can be varied are changed and the experiments are done keeping other factors constant. However, this method is very expensive and time-consuming.
5. Expert Opinion Method
Usually, the market experts have explicit knowledge about the factors affecting the demand. Their opinion can help in demand forecasting. The Delphi technique, developed by Olaf Helmer is one such method.
Under this method, experts are given a series of carefully designed questionnaires and are asked to forecast the demand. They are also required to give the suitable reasons. The opinions are shared with the experts to arrive at a conclusion. This is a fast and cheap technique.
6. Statistical Methods
The statistical method is one of the important methods of demand forecasting. Statistical methods are scientific, reliable and free from biases. The major statistical methods used for demand forecasting are:
- Trend Projection Method: This method is useful where the organization has sufficient amount of accumulated past data of the sales. This date is arranged chronologically to obtain a time series. Thus, the time series depicts the past trend and on the basis of it, the future market trend can be predicted. It is assumed that the past trend will continue in future. Thus, on the basis of the predicted future trend, the demand for a product or service is forecasted.
- Regression Analysis: This method establishes a relationship between the dependent variable and the independent variables. In our case, the quantity demanded is the dependent variable and income, the price of goods, price of related goods, the price of substitute goods, etc. are independent variables. The regression equation is derived assuming the relationship to be linear. Regression Equation: Y = a + bX. Where Y is the forecasted demand for a product or service.
Benefits of Forecasting:
It enables managers to visualize and discount future to the present. It, thus, improves the quality of planning. Planning is done for future under certain known conditions and forecasting helps in knowing these conditions. It provides knowledge of planning premises with which managers can analyse their strengths and weaknesses and take action to meet the requirements of the future market.
For example, if the TV manufacturers feel that LCD or Plasma televisions will replace the traditional televisions, they should take action to either change their product mix or start manufacturing LCD/Plasma screens. Forecasting, thus, helps in utilizing resources in the best and most profitable business areas.
In the fast changing technological world, businesses may find it difficult to survive if they do not forecast customers’ needs and competitors’ moves.
- Identification of critical areas
Forecasting helps in identifying areas that need managerial attention. It saves the company from incurring losses because of bad planning or ill defined objectives. By identifying critical areas of management and forecasting the requirement of different resources like money, men, material etc., managers can formulate better objectives and policies for the organisation. Forecasting, thus, increases organisational and managerial efficiency in terms of framing and implementing organisational plans and policies.
Though forecasting cannot eliminate risk, it reduces it substantially by estimating the direction in which environmental factors are moving. It helps the organisation survive in the uncertain environment by providing clues about what is going to happen in future.
If managers know in advance about changes in consumer preferences, they will bring required modifications in their product design in order to meet the changed expectations of the consumers. Thus, forecasting cannot stop the future changes from happening but it can prepare the organisations to face them when they occur or avoid them, if they can.
Forecasting involves participation of organisational members of all departments at all levels. It helps in coordinating departmental plans of the organisation at all levels. People in all departments at all levels are actively involved in coordinating business operations with likely future changes predicted as a result of forecasting. Thus, forecasting helps in movement of all the plans in the same direction.
By identifying the critical areas of functioning, managers can formulate sound objectives and policies for their organisations. This increases organisational efficiency, effectiveness in achieving the plans, better management and effective goal attainment.
- Development of executives
Forecasting develops the mental, conceptual and analytical abilities of executives to do things in planned, systematic and scientific manner. This helps to develop management executives.
Like this:
Like Loading...