There are problems where certain facilities have to be assigned to a number of jobs so as to maximize the overall performance of the assignment. The problem can be converted into a minimization problem in the following ways and then Hungarian method can be used for its solution.
- Change the signs of all values given in the table.
- Select the highest element in the entire assignment table and subtract all the elements of the table from the highest element.
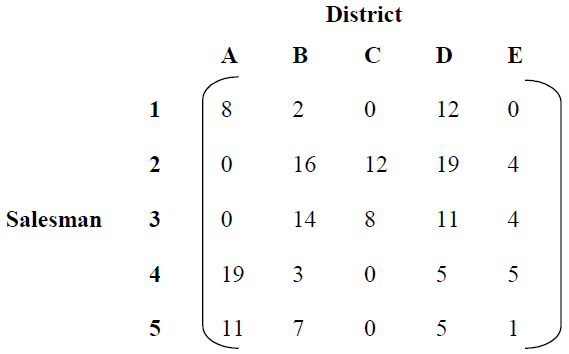
Example: A marketing manager has five salesmen and sales districts. Considering the capabilities of the salesmen and the nature of districts, the marketing manager estimates that sales per month (in hundred rupees) for each salesman in each district would be as follows. Find the assignment of salesmen to districts that will result in maximum sales.
Maximization Problem

Maximization assignment problem is transformed into minimization problem by
Solution: The given maximization problem is converted into minimization problem by subtracting from the highest sales value (i.e., 41) with all elements of the given table.
Conversion to Minimization Problem

Reduce the matrix row-wise
Matrix Reduced Row-wise
Reduce the matrix column-wise and draw minimum number of lines to cover all the zeros in the matrix, as shown in Table.
Matrix Reduced Column-wise and Zeros Covered

Number of lines drawn ≠ Order of matrix. Hence not optimal.
Select the least uncovered element, i.e., 4 and subtract it from other uncovered elements, add it to the elements at intersection of line and leave the elements that are covered with single line unchanged, Table.
Added & Subtracted the least Uncovered Element

Now, number of lines drawn = Order of matrix, hence optimality is reached. There are two alternative assignments due to presence of zero elements in cells (4, C), (4, D), (5, C) and (5, D).
Two Alternative Assignments
Therefore,
|
Assignment 1 |
Assignment 2 |
||||
|
Salesman |
Districts |
Sales (Rs.) |
Salesman |
Districts |
Sales (Rs.) |
| 1 | B | 38 | 1 | B | 38 |
| 2 | A | 40 | 2 | E | 36 |
| 3 | E | 37 | 3 | A | 41 |
| 4 | C | 41 | 4 | C | 41 |
| 5 | D | 35 | 5 | D | 35 |
| Total Rs. = 191.00 | Total Rs. = 191.00 | ||||