Security Market Line

Security market line (SML) is the representation of the capital asset pricing model. It displays the expected rate of return of an individual security as a function of systematic, non-diversifiable risk. The risk of an individual risky security reflects the volatility of the return from security rather than the return of the market portfolio. The risk in these individual risky securities reflects the systematic risk.

Formula

The Y-intercept of the SML is equal to the risk-free interest rate. The slope of the SML is equal to the market risk premium and reflects the risk return tradeoff at a given time:

E(R_i) = R_F + β_i × (E(R_M) – R_F)

Where:

E(Ri) is an expected return on security

E(RM) is an expected return on market portfolio M

β is a nondiversifiable or systematic risk

RM is a market rate of return

Rf is a risk-free rate

When used in portfolio management, the SML represents the investment’s opportunity cost (investing in a combination of the market portfolio and the risk-free asset). All the correctly priced securities are plotted on the SML. The assets above the line are undervalued because for a given amount of risk (beta), they yield a higher return. The assets below the line are overvalued because for a given amount of risk, they yield a lower return. In a market in perfect equilibrium, all securities would fall on the SML.

There is a question about what the SML looks like when beta is negative. A rational investor will accept these assets even though they yield sub-risk-free returns, because they will provide “recession insurance” as part of a well-diversified portfolio. Therefore, the SML continues in a straight line whether beta is positive or negative. A different way of thinking about this is that the absolute value of beta represents the amount of risk associated with the asset, while the sign explains when the risk occur.

SML Graph

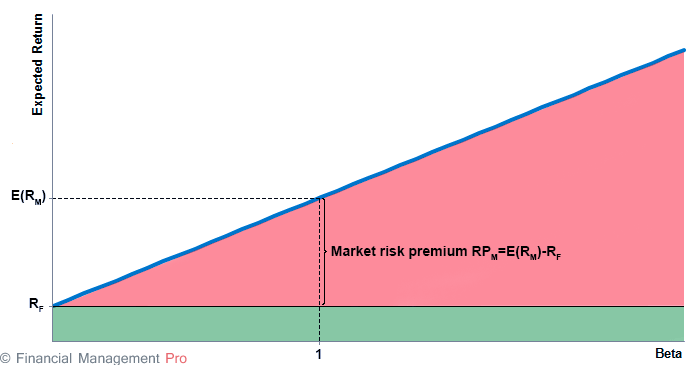
The x-axis of the SML graph is represented by the beta, and the y-axis is represented by the expected return. The value of the risk-free rate is the beginning of the line.

• The zero-beta security will have the expected return equal to the risk-free rate. The expected return of zero-beta portfolio also equals the risk-free rate.
• The slope of the security market line is determined by the market risk premium (RPM), which is the difference between the expected market return and the risk-free rate. The higher the market risk premium, the steeper the slope and vice versa.
• The SML is not fixed and can change the slope and y-axis intersection over time. It depends on changes in interest rates, risk-return trade-off.
• If the beta coefficient of the given security changes over time, its position on the line will also change.

The shift of SML can also occur when key economical fundamental factors change, such as a change in the expected inflation rate, GDP, or unemployment rate.