Black – Scholes Option Pricing Model
15/10/2020The Black Scholes model, also known as the Black-Scholes-Merton (BSM) model, is a mathematical model for pricing an options contract. In particular, the model estimates the variation over time of financial instruments. It assumes these instruments (such as stocks or futures) will have a lognormal distribution of prices. Using this assumption and factoring in other important variables, the equation derives the price of a call option.
Basics of the Black Scholes Model
The model assumes the price of heavily traded assets follows a geometric Brownian motion with constant drift and volatility. When applied to a stock option, the model incorporates the constant price variation of the stock, the time value of money, the option’s strike price, and the time to the option’s expiry.
Also called Black-Scholes-Merton, it was the first widely used model for option pricing. It’s used to calculate the theoretical value of options using current stock prices, expected dividends, the option’s strike price, expected interest rates, time to expiration and expected volatility.
The formula, developed by three economists Fischer Black, Myron Scholes and Robert Merton is perhaps the world’s most well-known options pricing model. The initial equation was introduced in Black and Scholes’ 1973 paper, “The Pricing of Options and Corporate Liabilities,” published in the Journal of Political Economy. Black passed away two years before Scholes and Merton were awarded the 1997 Nobel Prize in economics for their work in finding a new method to determine the value of derivatives (the Nobel Prize is not given posthumously; however, the Nobel committee acknowledged Black’s role in the Black-Scholes model).
The Black-Scholes model makes certain assumptions:
- The option is European and can only be exercised at expiration.
- No dividends are paid out during the life of the option.
- Markets are efficient (i.e., market movements cannot be predicted).
- There are no transaction costs in buying the option.
- The risk-free rate and volatility of the underlying are known and constant.
- The returns on the underlying asset are normally distributed.
While the original Black-Scholes model didn’t consider the effects of dividends paid during the life of the option, the model is frequently adapted to account for dividends by determining the ex-dividend date value of the underlying stock.
The Black Scholes Formula
The mathematics involved in the formula are complicated and can be intimidating. Fortunately, you don’t need to know or even understand the math to use Black-Scholes modeling in your own strategies. Options traders have access to a variety of online options calculators, and many of today’s trading platforms boast robust options analysis tools, including indicators and spreadsheets that perform the calculations and output the options pricing values.
The Black Scholes call option formula is calculated by multiplying the stock price by the cumulative standard normal probability distribution function. Thereafter, the net present value (NPV) of the strike price multiplied by the cumulative standard normal distribution is subtracted from the resulting value of the previous calculation.
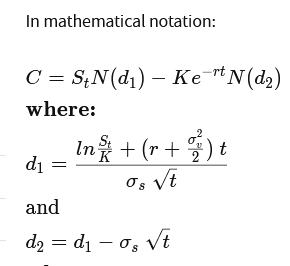
where:
C=Call option price
S=Current stock (or other underlying) price
K=Strike price
r=Risk-free interest rate
t=Time to maturity
N=A normal distribution
[…] VIEW […]